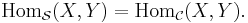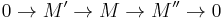Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and arrows.
Contents |
Formal definition
Let C be a category. A subcategory S of C is given by
- a subcollection of objects of C, denoted ob(S),
- a subcollection of morphisms of C, denoted hom(S).
such that
- for every X in ob(S), the identity morphism idX is in hom(S),
- for every morphism f : X → Y in hom(S), both the source X and the target Y are in ob(S),
- for every pair of morphisms f and g in hom(S) the composite f o g is in hom(S) whenever it is defined.
These conditions ensure that S is a category in its own right. There is an obvious faithful functor I : S → C, called the inclusion functor which is just the identity on objects and morphisms.
Let S be a subcategory of a category C. We say that S is a full subcategory of C if for each pair of objects X and Y of S
A full subcategory is one that includes all morphisms between objects of S. For any collection of objects A in C, there is a unique full subcategory of C whose objects are those in A.
Embeddings
Given a subcategory S of C the inclusion functor I : S → C is both faithful and injective on objects. It is full if and only if S is a full subcategory.
Many authors define an embedding to be a full and faithful functor.[1]
Other authors define a functor to be an embedding if it is faithful and injective on objects. Equivalently, F is an embedding if it is injective on morphisms. A functor F is then called a full embedding if it is a full functor and an embedding.
For any (full) embedding F : B → C the image of F is a (full) subcategory S of C and F induces a isomorphism of categories between B and S.
In some categories, one can also speak of morphisms of the category being embeddings.
Types of subcategories
A subcategory S of C is said to be isomorphism-closed or replete if every isomorphism k : X → Y in C such that Y is in S also belongs to S. A isomorphism-closed full subcategory is said to be strictly full.
A subcategory of C is wide or lluf (a term first posed by P. Freyd[2]) if it contains all the objects of C. A lluf subcategory is typically not full: the only full lluf subcategory of a category is that category itself.
A Serre subcategory is a non-empty full subcategory S of an abelian category C such that for all short exact sequences
in C, M belongs to S if and only if both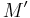 
and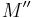 
do. This notion arises from Serre's C-theory.
References
- ^ van Oosten. "Basic category theory". http://www.staff.science.uu.nl/~ooste110/syllabi/catsmoeder.pdf.
- ^ Freyd, Peter (1990). "Algebraically complete categories". LNCS 1488. "Proc. Category Theory, Como"